Cryptographic Hash Functions

Welcome to my first substack! 👋 As I journey into the realm of Bitcoin my hope is to learn, build and share as much as possible in a way that helps others onboard into the Bitcoin ecosystem easily. I find that too often “explainer” articles are not really beginner friendly and I am going to do my bit for the Bitcoin ecosystem by utilizing my computer science background (Bsc (with honors) degree/work experience) and passion for this space/education to endeavor to bridge this gap. I see huge potential in the future for crypto as a whole and I believe that in order to achieve the future we all want (Financial Sovereignty, Decentralisation, Global inclusivity/solidarity, Transparency, and trust), we must all play our part to educate, enlighten and guide our society collectively in the right direction.

If this article only manages to help one person, I will consider my time well spent.

"We don't have to engage in grand, heroic actions to participate in change. Small acts, when multiplied by millions of people, can transform the world." - Howard Zinn

---

In this article, I will explain cryptographic hash functions, what they are, how they work, what their properties are, what their applications are, and why they are vital for the Bitcoin blockchain, which uses a hash called SHA-256 that returns a fixed string of numbers and letters, specifically 64 characters long or 32 bytes, which is equivalent to 256 bits. [1]

What is a Cryptographic Hash Function and how do they work?

A cryptographic hash function is a special and usually extremely complex mathematical algorithm that takes any type of data, such as a text message or a file (image/music/pdf, etc..), and transforms it into a unique fixed-size string of characters, which is often a series of numbers and letters. In the case of SHA-256, the returned string is irreversible meaning the original input cannot be determined by the output. This is different from cryptographic hashes that are referred to as “Trapdoor”. Trapdoor functions are often used in public-key cryptography systems like RSA, where the trapdoor enables efficient decryption of the encrypted message. However, SHA-256 is a one-way cryptographic hash function. [2]. To check the validity of any data received, we need only compare the two hashes.

For example, let’s take the following string (a sequence of characters) and hash it using the SHA-256 algorithm:

string:

This is a secret message hashed using SHA-256

returned hash:

    3cb41afffffc58ee608b997073c96bf739dbf651ee50be33ef079d4bc8495657

The hash function will always return the same hash for the same input. This is because it is what is referred to as a deterministic function. Determinism is a crucial aspect of cryptographic hash functions (like SHA-256) because it enables the consistent and predictable generation of hash values (like the example above). It ensures that the same input will always produce the same output. This is essential for various security applications such as data integrity checking, password storage (never store an unhashed password online), and digital signatures.

So, if the value returned from a string will always be the same, can you tell me why this same string below returns a completely different hash?

string:

This is a secret message hashed using sha-256

returned hash:

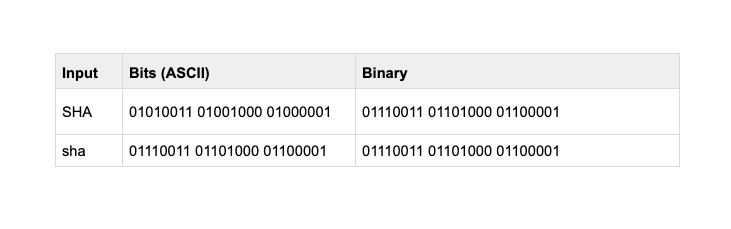
    7d25da85c5e7b752e1b9ad69c41ac407e76e3d32351fcbbbafbfe26868e8f790

Ok, you got me there. The string isn’t actually the same. Not to a computer anyway. As you can see, I changed SHA to sha. This is because computers use binary representation to store and manipulate data, perform calculations, and execute instructions.

All data, including numbers, characters, images, audio, etc.., can be represented using binary digits. Each bit represents a binary digit (0 or 1), and groups of bits form what we call bytes, which can represent larger units of data.

In binary representation, each character is typically encoded using a character encoding scheme, such as ASCII or Unicode. These encoding schemes assign numeric values to characters, which are then represented (read by the computer) in binary form.

For example, let's consider the ASCII encoding scheme. In ASCII, each character is represented by a unique 7-bit binary code. When converting a character to binary, the corresponding ASCII code is determined, and that code is then represented in binary form.

ASCII codes, or ASCII (American Standard Code for Information Interchange), is a character encoding scheme that represents characters as numeric codes. It is a widely used encoding system that assigns unique numeric values to a set of characters commonly used in English and other Western languages. [3]

The table below shows the difference in Binary and ASCII for the inputs SHA and sha. As you can see, the computer reads them completely differently - even if our human eyes understand them to be the same, a computer will not.

I felt the need to mention this because I have made this mistake thousands of times in my history of being a developer where I have overlooked capitalized characters and have pulled out my hair not understanding why the outputs are not as expected. I hope I can spare you the same pain in the future.

What are the properties of a Hash Function?

As you can probably imagine, there are some important and vital properties needed in a hash function in order for it to be secure and useful:

• Efficiently computable

• Collision-free

• Hiding (pigeonhole)

Efficiently computable

A hash function needs to be “efficiently computable” which means it can process inputs of various sizes, ranging from small to very large, and produce the hash value in a reasonable time frame. To achieve this the following must be considered:

• The speed of reliable computation,

• The complexity of the algorithm,

• Scalability of the hash function with regard to the input size.

The speed of reliable computation

The speed of reliable computation is a critical property of a hash function like SHA-256. It ensures that the function can process data efficiently and produce hash values within a reasonable timeframe. By being able to quickly generate hash values, SHA-256 enables real-time or high-performance applications where data integrity and security are paramount. Its speed allows for the seamless integration of hash functions into various systems and processes, facilitating smooth and efficient operations.

The complexity of the algorithm

The complexity of the algorithm employed by a hash function is a fundamental aspect of ensuring robust security. SHA-256's algorithm is designed to be mathematically intricate, making it difficult for attackers to reverse-engineer the original input from the hash value or identify any patterns that could compromise security. The complexity adds a layer of defense against cryptographic attacks, providing confidence in the integrity and reliability of the hash function's output. The algorithm of SHA-256 contributes to its resilience against various known cryptographic vulnerabilities by utilizing: Collision Resistance, Preimage Resistance and Mathematical Complexity [4]

Scalability of the hash function with regard to the input size.

Scalability is really important for a hash function like SHA-256 because it allows you to use it with inputs of different sizes. It doesn't matter if the data is small or large, SHA-256 can handle it well and give consistent and reliable results.

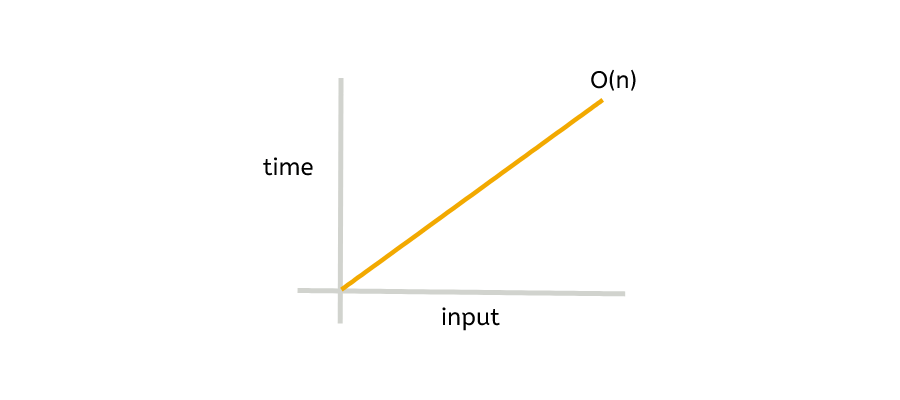
In computer science, the algorithm’s scalability is measured with something referred to as Time Complexity. This does not consider the computational resources available. Time complexity analysis focuses solely on algorithmic behavior. [5]

The time complexity of SHA-256 is commonly considered to be O(n), where n represents the size of the input message or data being hashed. This means the runtime grows linearly with the size of the input.

Collision-free

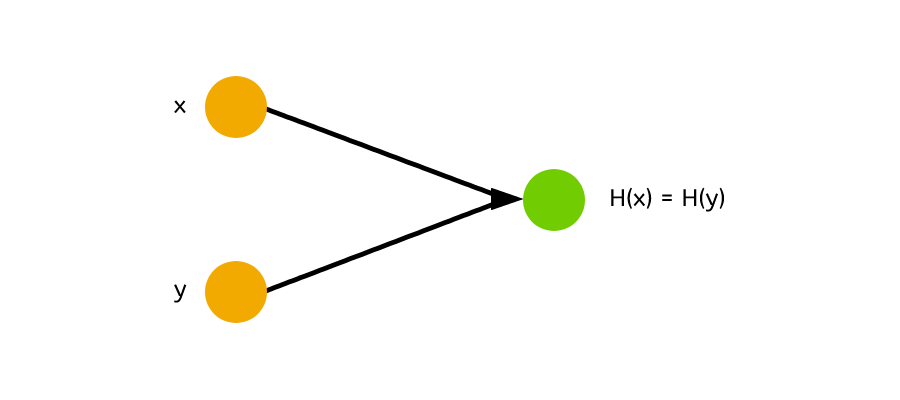
In order to understand what is meant by collision-free, it’s probably best I explain what a collision is first.

A collision in simple terms is when two inputs result in the same output. When the input value of x and the input value of y both return the same result. h(x) = h(y)

A collision is bad for a cryptographic hash function because we want to be able to distinguish the difference in input and we also want to make it harder for the attacker to be able to guess what the input is.

Hiding and the Pigeonhole principle

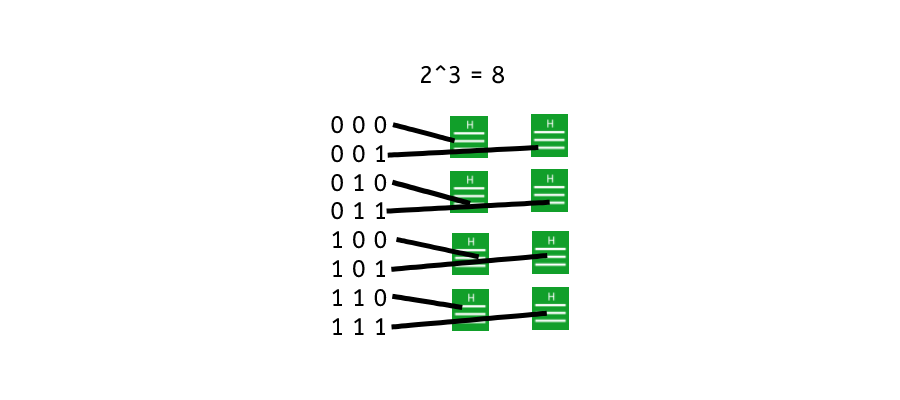
The pigeonhole principle is a mathematical concept that states that if n items are put into m containers, with n > m, then at least one container must contain more than one item. Or in simple pigeon terms, If you have 10 pigeon holes but you have 15 pigeons. It’s relatively safe to assume that 1 or more pigeons will go through the same hole.

In another example let’s say you have a 3-bit hash function. This means it takes a length of 3. Each possible bit can be either 1 or 0. A binary input. That means you have 8 possible combinations as 2^3 = 8. 2(bits) and 3(input slots).

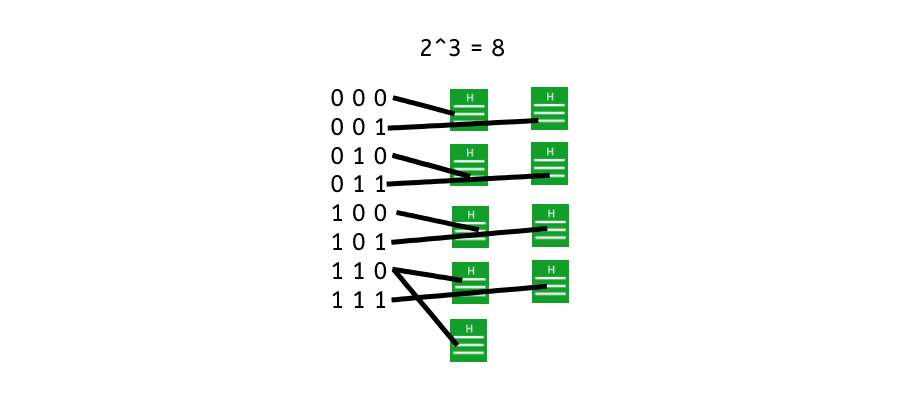
If we run 8 different combinations into the function we will get 8 different outputs. However, because the pool of inputs is so small. Running an extra test, a 9th input will then result in one of the hashed being returned as the same.

With a small input space, such as the 3-bit hash function example, it becomes feasible to find collisions and potentially determine the original input. However, by increasing the size of the possible input space (using longer bit lengths), the resources and computational effort required to find collisions become significantly impractical, enhancing the cryptographic security of the hash function. [6]

Let’s say we build our own hash function. It’s very simple. It takes an input n, gets the length of that input l(n), and then performs a simple module 3 calculation on it. The result would be the same:

1. Name: "John"

   • Length: 4

   • Hash value: 4 % 3 = 1

2. Name: "Josh"

   • Length: 4

   • Hash value: 4 % 3 = 1

The returning hash would be a collision because we clearly have two separate inputs but the hash has generated the same output.

A better way (a primitive example) would be to calculate the sum of the ASCII values of each letter first (as mentioned earlier a computer would see each letter differently) and then perform the modulo 3 calculation.

1. Name: "John"

   • ASCII values: J (74), o (111), h (104), n (110)

   • Sum of ASCII values: 74 + 111 + 104 + 110 = 399

   • Hash value: 399 % 3 = 0

2. Name: "Josh"

   • ASCII values: J (74), o (111), s (115), h (104)

   • Sum of ASCII values: 74 + 111 + 115 + 104 = 404

   • Hash value: 404 % 3 = 2

How is this achieved in Bitcoin?

Quite simply, bitcoin uses a large amount of data, called the large digest which as we’ve proven above means it avoids collisions. The data that goes into signing a transaction for example is:

1. Block Header: Containing essential information about the block such as its version, a timestamp, previous block hash, and difficulty target. These header fields ensure the proper sequencing and linkage of blocks in the blockchain.

2. Merkle Root: The Merkle root is a hash of all the transactions within the block. It is calculated by hashing each transaction individually, pairing them up, hashing the pairs together, and repeating this process until a single hash, known as the Merkle root, is obtained.

3. Nonce: The nonce is a random value included in the block header. Miners modify this value during the mining process to try different combinations and find a valid hash that meets the target difficulty. The nonce allows for the generation of different hash outputs.

4. Additional data: There is also additional data added to the block, some of it could be random and some could be anonymous (like sender information)

As you can see, the sheer amount of data that is processed and hashed, including hashes of other parts and random values makes it computationally infeasible to reverse.

Another factor that the Bitcoin network does is it imposes a time constraint. Every 10 mins a new block will be created. Meaning all those hashes that were created will be changed as the new block will contain the previous block data. This means if some bad actor wanted to gain control of the Bitcoin network and insert a false transaction they would have 10 minutes to computationally work out every piece of data. After a new block is created, any transaction trying to insert into a previous block would automatically be rejected.

So, if it’s unfeasible to reverse this, how does Bitcoin verify the transaction or data is true? Well, the Bitcoin network isn’t trying to attack itself, it’s only trying to validate that the data it has received is accurate. We pass the required data to the network to ease its computational stress.

Verifying inputs: Hash as a message digest

Using a cryptographic hash to verify content reliability is an extremely useful tool. Without it, let’s say you received a file. The file is the Bitcoin whitepaper in pdf [7] format.

You later receive from an unknown source another Bitcoin whitepaper pdf. To check the validity and consistency of data within these files without a hash you would need to open the files and check every single character one by one. An extremely tedious task.

However, if you check the hash of the first file, which btw is:

    B1674191A88EC5CDD733E4240A81803105DC412D6C6708D53AB94FC248F4F553

and then you check the hash of the second file and it returns the same hash then you can be sure that they are both the same without nefarious actors tampering with the data. This is useful because the returned is only 256-bits in length which makes it faster and easier to compare and verify.

In terms of a Bitcoin transaction, we are also passing the values required to verify this is true. This is referred to as Commitment. Because in Bitcoin we only need to verify the correct output and we are not trying to attack the system. We commit a message to the blockchain and the blockchain will verify, known as the function verify.

The commitment and verification formulas are based on the concept of using a cryptographic hash function and a secret key to create and verify commitments.

Let’s assume the following:

1. key = “SuperSecretKey0123”

2. msg = “My Super Secret Message”

Commitment Formula: The commitment formula:

   commit(msg) = (H(key | msg), key) 

involves two main components:

1. H(key | msg): The "|" symbol denotes concatenation (or joining together), so H(key | msg) represents the concatenation of the secret key (key) with the message (msg). The resulting concatenated string is then input into the cryptographic hash function H. The hash function processes the combined input and produces a fixed-length hash output, which serves as the commitment to the message. Using our values above:

   1. H(key | msg): Concatenating the key and message, we have "SuperSecretKey0123My Super Secret Message".

   2. Hash Calculation: Apply SHA-256 hash to the concatenated string returns the resulting hash of: 5e01d8f19aa3352e8a9c3b2a27d13a3818d0b3d8e0c9f071b1f43b2f7c2ff4e5

   3. H((key | msg), key): we then use the key to has together which is “5e01d8f19aa3352e8a9c3b2a27d13a3818d0b3d8e0c9f071b1f43b2f7c2ff4e5, SuperSecretKey0123”

2. key: The secret key (key) is included along with the hash output. This key is typically known only to the sender or a specific party involved in the commitment process. It is used during the verification phase to ensure that the commitment can be verified correctly.

This means that our commit = 9251e642a42f8c8d98b66bc9deff4866d84e3a45e3e604d27a4bead6cdebf4d1

So we pass to the verify formula verify(commit, key, msg):

1. key = “SuperSecretKey0123”

2. msg = “My Super Secret Message”

3. commit = “9251e642a42f8c8d98b66bc9deff4866d84e3a45e3e604d27a4bead6cdebf4d1”

Verification Formula: The verification formula, verify(commit, key, msg) = (H(key | msg) == commit), checks the validity of a given commitment, message, and key. It involves the following steps:

1. H(key | msg): Similar to the commitment formula, H(key | msg) represents the hash of the concatenated secret key and message. This step produces the same hash value as in the commitment phase.

2. H(key | msg) == commit: This step compares the hash output (H(key | msg)) with the provided commitment (commit). If the two values match, it indicates that the commitment is valid and has not been tampered with.

If the output hash of commit and the output of verify are both the same. We know the transaction to be true.

Because we have successfully randomized the inputs and made it extremely difficult to guess the input we can verify that no collisions have taken place.

Multiple nodes on the Bitcoin transaction will verify this transaction and when the network reaches consensus - which is more than 51% of the network agrees the verification is accurate, it will be added to the blockchain.

and the whole process will start again for the next block.

commit, verify, repeat.

I asked chatGPT to check the accuracy of my work. It said I oversimplified the verification and commitment part of Bitcoin and suggested the following (adding in case it helps):

Imagine you want to send a secret message to your friend and you want to make sure that no one else can change the message or pretend to be you. You also want to prove later on that the message you sent is authentic. This is where the concepts of “commitment” and “verification” come into play.

Commitment:

1. Think of this step as sealing your message in a magic box. You take your secret message and add a special password (key) to it.

2. Then, you use a special mathematical recipe (a hash function like SHA-256) to turn this combination into a scrambled code. This scrambled code is your commitment - it’s like the locked magic box that keeps your secret message safe.

Verification:

1. When your friend receives the magic box, he wants to make sure it’s really from you and hasn’t been tampered with.

2. To do this, your friend uses the same mathematical recipe, the password (key), and the original message you sent.

3. He creates a new scrambled code and compares it to the one in the magic box. If the codes match, it means the message is authentic!

If you have any specific questions or general comments, please feel free to ping me on Twitter: https://twitter.com/web3withmark

References:

1. Bitcoin Wiki. (n.d.). Block hashing algorithm. Available at: https://en.bitcoin.it/wiki/Block_hashing_algorithm [Accessed 18 June 2023].

2. Wikipedia. (n.d.). Trapdoor function. Available at: https://en.wikipedia.org/wiki/Trapdoor_function [Accessed 18 June 2023].

3. ASCII Code. (n.d.). The extended ASCII table. Available at:

   https://www.ascii-code.com/ [Accessed 18 June 2023].

4. Coron, J. & Prouff, E. (2019). ‘On the Influence of the Algebraic Degree of 𝑥 + 𝑥^𝑝 on the Differential Properties of 𝑓(𝑥) = 𝑥 + 𝑥^𝑝’. IACR Cryptology ePrint Archive, [pdf] Available at: https://eprint.iacr.org/2019/686.pdf [Accessed 18 June 2023].

5. My Great Learning. (n.d.). Why is Time Complexity Essential? Available at: https://www.mygreatlearning.com/blog/why-is-time-complexity-essential/#:~:text=Time%20complexity%20is%20defined%20as,of%20code%20in%20an%20algorithm [Accessed 18 June 2023].

6. 3Blue1Brown. (2017). But how does bitcoin actually work? [Video] Available at: https://-youtu.be/HHQ2QP_upGM?t=468 [Accessed 18 June 2023].

7. Nakamoto, S. (2008). Bitcoin: A Peer-to-Peer Electronic Cash System. [pdf] Available at: https://bitcoin.org/bitcoin.pdf [Accessed 18 June 2023].